Overview
Sharemind Technology
Sharemind is a privacy-preserving database and analysis system that allows you to combine confidential data from several sources and analyse it without ever seeing the data itself. It also allows data owners and interested third parties to enforce data usage policies.
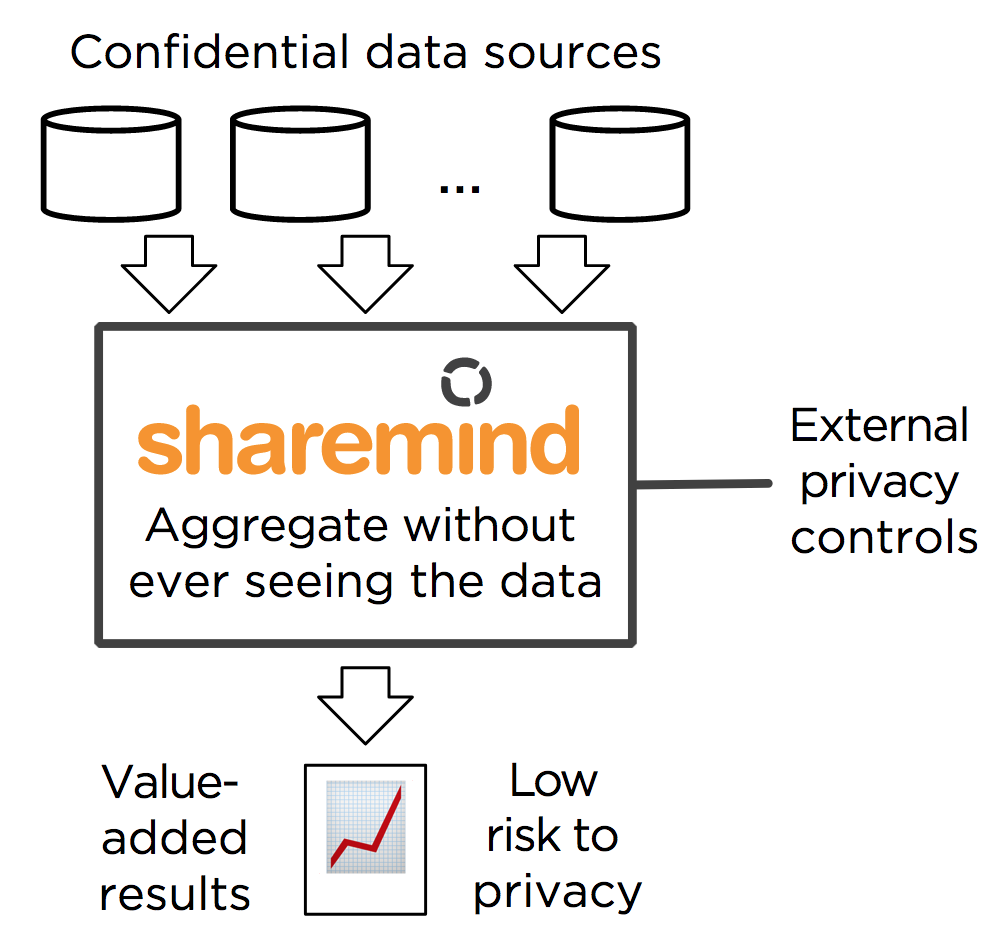
Three independent Sharemind hosts run the Sharemind MPC software. Data Owners share their data between the three Sharemind Hosts, resulting in a distributed database. Analysts can query this database, but only with the approval of Enforcers who verify that the query conforms to the data usage policy.
Sharemind MPC achieves privacy by using cryptographic secret sharing and secure multi-party computation (MPC).
Secure multi-party computation
Secure multi-party computation (MPC, also abbreviated as SMC) is a technique for evaluating a function with multiple peers so that each of them learns the output value but not each other’s inputs. There are various ways for implementing secure MPC with different number of peers and security guarantees. Here, we concentrate on systems based on secret sharing.
Share computing systems use the concept of secret sharing introduced by Blakley (Blakley, 1979) and Shamir (Shamir, 1979). In secret sharing, a secret value \(s\) is split into any number of shares \(s_1\), \(s_2\), \(\ldots\), \(s_n\) that are distributed among the peers (computing nodes). Depending on the type of scheme used, the original value can be reconstructed only by knowing all or a predefined number (threshold \(t\)) of these shares. Any group of \(t\) or more peers can combine their shares to reconstruct the original value. However, the result of combining less than \(t\) shares provides no information about the value they represent.
Secure multi-party computation protocols can be used to process secret-shared data. These protocols take secret-shared values as inputs and output a secret-shared result that can be used in further computations. For example, let us have values \(u\) and \(v\) that are both secret-shared and distributed among all the peers so that each computation node \(\mathcal{C}_i\) gets the shares \(u_i\) and \(v_i\). To evaluate \(w = u \oplus v\) for some binary function \(\oplus\), the computation nodes engage in a share computing protocol and output \(w\) in a shared form (node \(\mathcal{C}_i\) holds \(w_i\)). During the computation, no computation node is able to recover the original values \(u\) or \(v\) nor learn anything about the output value \(w\).
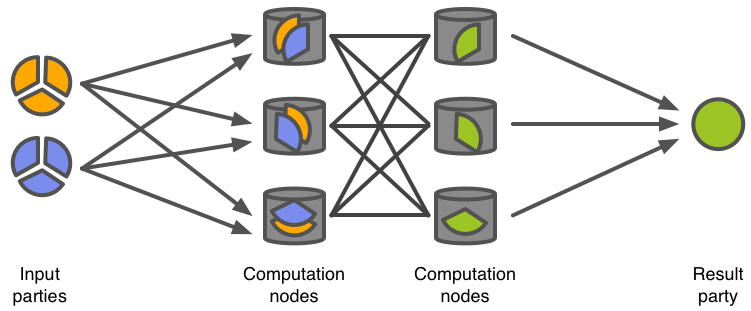
The fact that most MPC protocols are composable and the computation result is also secret-shared, allows one to use the output of one computation as an input for the next one. Using this property, one can combine primitive functions like multiplication or comparison into algorithms (e.g. sorting) and such algorithms into applications that implement the necessary business logic in privacy-preserving fashion.
Multi-party computation protocols can be secure in either passive or active corruption models. In the passive model, an adversary can read all the information available to the corrupted peer, but it cannot modify it. In this case, the corrupted peer still follows the predefined protocol, but it tries to deduce the original data values based on the information available to that peer. This is also known as honest-but-curious model. In the active model, an adversary has full control over the corrupted peer. For more properties of MPC protocols, see [1].
Sharemind MPC
Sharemind MPC is a practical implementation of secure multi-party computation technology with the emphasis on performance and ease of use. Sharemind MPC supports several different MPC schemes called protection domains, with the shared3p protection domain being the most advanced one. It stands for 3-out-of-3 secret sharing with passive security and uses additive secret sharing scheme, where a secret value \(s\) is secret shared as follows:
such that \(s = s_1 + s_2 + s_3\). All these computations are done
modulo the corresponding data type size, e.g. modulo \(2^{64}\) for
64-bit (unsigned) integers. Note that this modulo computation happens
automatically for primitive data types like (u)int8, (u)int16,
(u)int32 and (u)int64. More complex data types (e.g. floating point
numbers) use structures of primitive data types.
As an example, suppose we have two Data Owners with their secret values – their ages 25 and 33 – and a third party – an Analyst – who wants to learn the sum of their ages.
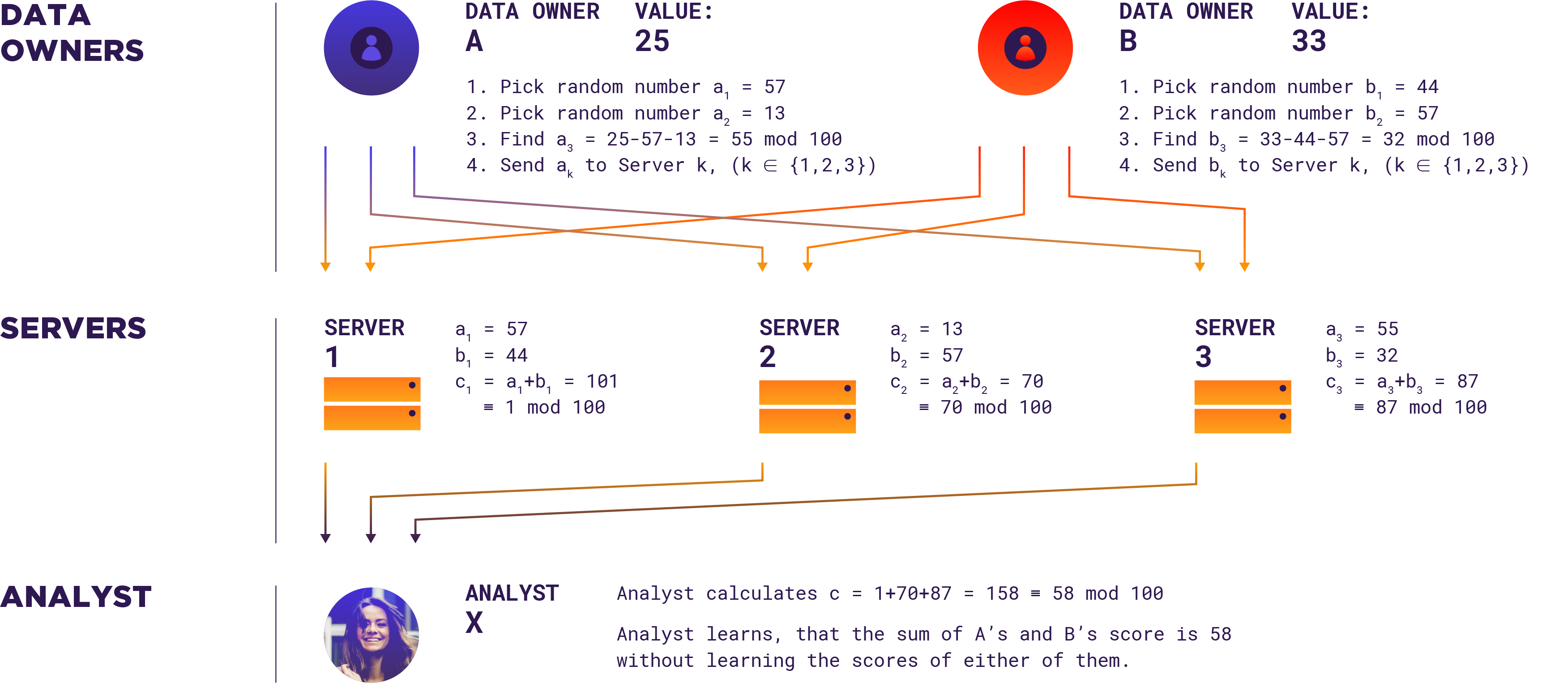
In additive secret sharing, to secret share her age, the first user picks two random numbers modulo 100. Let these be 57 and 13. The third share is computed by subtracting the random values from the secret value. 25 minus 57 minus 13 is -45, but modulo 100 it is the same as 55. The Data Owner now distributes these three shares – 57, 13 and 55 – between the three Sharemind hosts over secure authenticated and encrypted communication channels. None of the shares alone, nor any pair of these shares give any information about the original secret value. However, note that by adding up all the three shares, it is possible to reconstruct the original value. The second Data Owner acts similarly, he first generates two random numbers – 44 and 57 – and then computes the third share by subtracting these from the secret value 33. He distributes the shares among the Sharemind hosts. With additive secret sharing, addition is a local operation so each Sharemind host can just locally sum together their shares from the Data Owners. The first Sharemind host computes 57 plus 44 which is 101 but that is equal to 1 modulo 100. And so on. Next, each Sharemind host sends its partial result to the Analyst.
Finally, the Analyst reconstructs the computation result by adding up the individual received shares. 1 plus 70 plus 87 is equal to 158 that is equal to 58 modulo 100. And 58 is exactly 25 plus 33! Analyst has learned the sum of two ages without him learning their individual secret values. Sharemind hosts haven’t learned anything about the secret values not the computation result.